|
function_world.jpg
(polus) (11.12.2016 13:28)
|
|
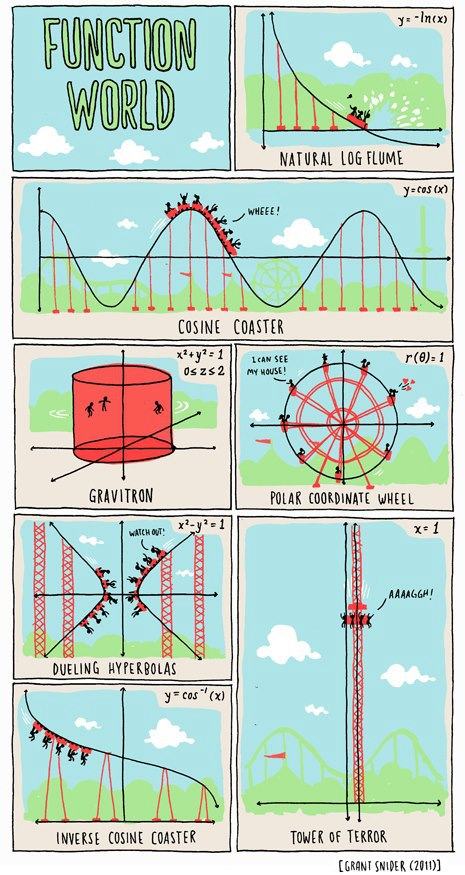
x^2+y^2=1 fukce dana implicitne. Navic nikde nejsou popsane osy! Pokud bereme prevedeni do systemu polarnich souradnic, tak je funkce snad vse. Cpt. out bitches. |
|
|
function_world.jpg
(ingotak) RP (25.3.2013 12:09)
|
Co je na kuloidních a jiných souřadnicích debilního?  vždyť se používají běžně vždyť se používají běžně  |
|
|
function_world.jpg
(JirkaCV) RP (25.3.2013 10:10)
|
|
To logáro jsem přehlídl, |
|
|
function_world.jpg
(JirkaCV) RP (25.3.2013 10:09)
|
|
Funkce jsou jenom ty cosiny. Ostatní funkce nejsou. Alespoň v kartézské soustavě souřadnic. V kuloidních a jiných debilních soustavách může být funkcí prakticky cokoliv. |
|
|
function_world.jpg
(BG) RP (25.3.2013 1:31)
|
|
neni to tak, ze ten graf je zlozeny z niekolkych funkcii, ktore zalezia to od parametra? |
|
|
function_world.jpg
(IanE) RP (25.3.2013 0:37)
|
|
ve kterém vesmíru je x^2+y^2=1 funkce podle x nebo y (což jsou jediné proměnné, které se v ní vyskytují)? |
|
|
function_world.jpg
(ingotak) RP (25.3.2013 0:25)
|
Proč by v polárních souřadnicích nemohla být taková funkce? Vždyť funkce může být v podstatě cokoli, pokud si dobře zvolíš proměnnou.... a lepší než x=1 by mohlo být y=δ(x-1)  |
|
|
function_world.jpg
(IanE) RP (24.3.2013 23:33)
|
|
Fascinuje mě, jak se všichni soustředí na to poslední, které opravdu funkcí může být, ale to že "Polar Coordinate Wheel" je nazýváno funkcí nikomu nevadí. |
|
|
function_world.jpg
(456) (24.3.2013 23:11)
|
takže y=ln(x) není funkce, protože pro některá iks není definovaná.  |
|
|
function_world.jpg
(Pichi) (24.3.2013 22:48)
|
|
Tady je to samej odborník. Co takhle parametrické funkce? To poslední není zobrazení x -> y, ale to neznamená, že to není zobrazení třeba z k -> x x y. |
|
|
function_world.jpg
(skylajner) RP (24.3.2013 22:30)
|
|
nicméně ty hyperboly fce takhle rozhodně nejsou, ani podle X ani podle Y - leda by byl otočenej souřadnej systém tak, že by řečené Y /dle konvence/ bylo rovnoběžné s asymptotou hyperboly |
|
|
function_world.jpg
(skylajner) RP (24.3.2013 22:29)
|
|
popřípadě je to f(y)=x... čili striktně matematicky to může bejt funkce naprosto vklidu, jen stačí pamatovat na pravidla počítání |
|
|
function_world.jpg
({}) (24.3.2013 22:19)
|
|
striktne matematicky, to posledne nie je funkcia - nesplna podmienku ze kazdemu bodu x priradi prave 1 bod y. Funkciou by to bolo, keby ta priamka mala iny ako zvisly smer. |
|
|
function_world.jpg
(kladivo) (24.3.2013 22:15)
|
|
Pff,x=1 neni funkce. |
|
 Komentáře (14)
Komentovat
Nezobrazovat
Komentáře (14)
Komentovat
Nezobrazovat
 vždyť se používají běžně
vždyť se používají běžně