|
priklad_2020_10_13.png
(Jakub1989) RP (14.10.2020 20:29)
|
|
8 |
|
|
priklad_2020_10_13.png
(Heretik) (14.10.2020 17:07)
|
|
Správnou úvahu, která nezávisí na konkrétních hodnotách, popsal @Kos.
Naopak cokoli, co počítá s pravoúhlým trojúhelníkem 3-4-5 obecně nefunguje, protože jen ve speciálním případě jako je tento je AC || DE. Představte si například, že |AB|=5 a |CD|=3. Pak je x pořád stejné, ale přes 3-4-5 trojúhelník už to nefunguje.
Délky můžou být libovolné, když zachováme označené pravé úhly, tak jediná podmínka je, aby |AE| bylo rovno buď |BC| nebo součtu |AB|+|CD|. |
|
|
priklad_2020_10_13.png
(tequila) RP (14.10.2020 16:39)
|
Kurva drát! Od kdy se značí pravý úhel takhle?!  |
|
|
priklad_2020_10_13.png
(paprik) (14.10.2020 12:48)
|
|
PJ:preco si myslis ze uhol CFD je pravouhly ? (ked dlzka CF je vysledok)? |
|
|
priklad_2020_10_13.png
(Kasuha) (14.10.2020 9:52)
|
|
x=8, stačí tu šikmou lomenici ozrcadlit kolem spojnice koncových bodů.
|
|
|
priklad_2020_10_13.png
(-satr-) RP (14.10.2020 9:05)
|
|
esteze je z obrázka zrejmé, že EBC ležia na jednej priamke. |
|
|
priklad_2020_10_13.png
(PJ) (14.10.2020 8:33)
|
|
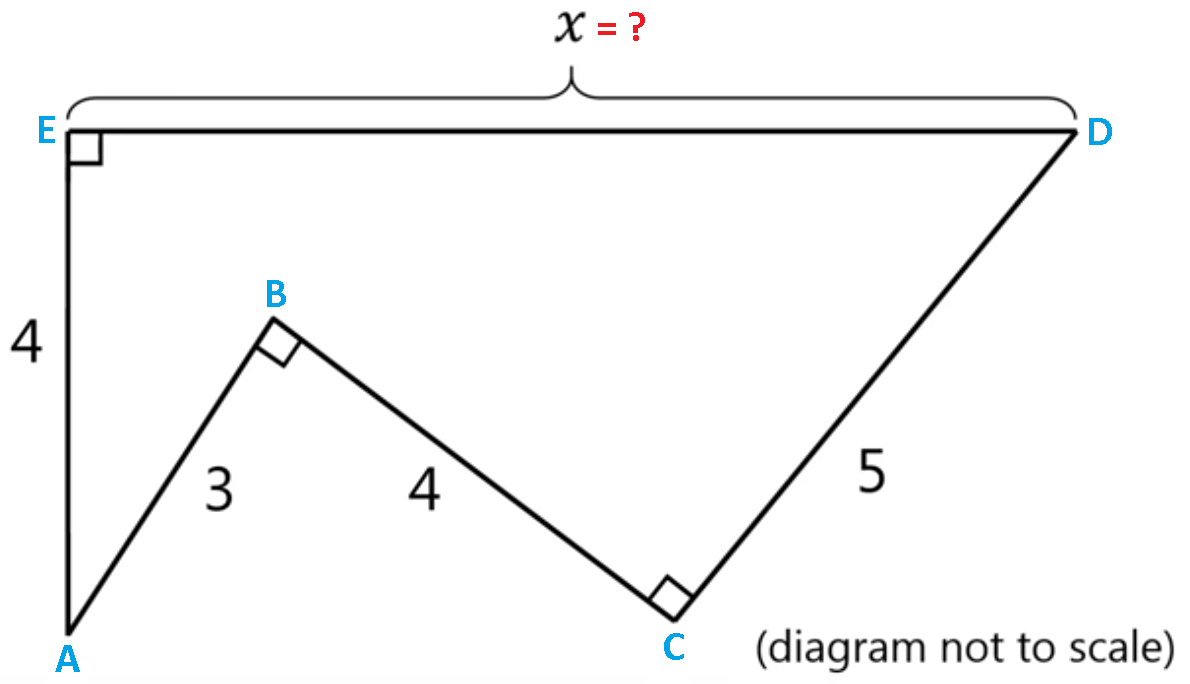
V tomto specialnom pripade: prenesme si EA do D tak, vznika nam bod F, takze mame obdlznik EDFA.
Lezi C na AF? Aby lezalo, tak musi byt trojuholnik CFD pravouhly (aby sa uhol zhodoval s uhlom obdlznika). Na pravouhlost CFD treba z Pytagorovej vety, aby CF boli 3.
Uz staci dopocitat AC, co je z Pytagorovej vety 5 a mame vysledok AC+CF=8 |
|
|
priklad_2020_10_13.png
(paprik) (14.10.2020 6:30)
|
|
Dr.Str.: Prečo je AC || ED ? |
|
|
priklad_2020_10_13.png
(Dr.Str.) RP (14.10.2020 5:49)
|
|
Už v Egyptě věděli, že trojúhelník o stranách 3,4,5 je pravoúhlý. Takže hrana AC=5 a odvěsna FD=3, takže X=8. |
|
|
priklad_2020_10_13.png
(zelenina) (14.10.2020 2:57)
|
Proc tohle nevychazi hezky?
|AE|^2 = |AB|^2 + |BE|^2
|BE| = sqrt(7)
x^2 = |EC|^2 + |CD|^2
x^2 = (|BE|+|BC ^2 + |CD|^2
x^2 = (sqrt(7)+4)^2 + 5^2
x = uplnej blabol |
|
|
priklad_2020_10_13.png
(pc2005) (13.10.2020 22:49)
|
|
Kos: ale tohle bude fungovat jen pro speciální případ, kdy je délka AE stejná jako BC |
|
|
priklad_2020_10_13.png
(Kos) (13.10.2020 22:32)
|
|
Netřeba ani počítat. Když protáheš DC dolů o 3 (nazvěme F), tak máme pravoúhlý trojúhelník ADF s odvěsnami 4 a 8 (AF,DF) a přeponou AD.
No a z druhé strany té přepony AD je stejný pravoúhlý trojúhelník AED s odvěsnami 4 a X.
X=8 |
|
|
priklad_2020_10_13.png
(pc2005) (13.10.2020 21:59)
|
|
By byl dobrej troll zrcadlit bod E podle osy AD. Vyjde to stejně (dokonce druhý řešení při konstrukci podle těch zadaných délek), ale je to mnohem míň intuitivní a člověka to hnedka nesvede to té rovnoběžnosti AC vs ED. |
|
|
priklad_2020_10_13.png
(RoflMao) RP (13.10.2020 20:16)
|
x = 8  |
|
|
priklad_2020_10_13.png
(Grifit) RP (13.10.2020 18:38)
|
|
a pro objem 8*4-3*4=(8-3)*4=5*4=20 |
|
