|
hadanka_na_nedeli.jpg
(tom_) (10.3.2022 21:49)
|
|
https://www.rouming.cz/roumingGIF.php?gif=72842 |
|
|
hadanka_na_nedeli.jpg
(Kapitan Bomba) (29.9.2020 20:32)
|
|
Vseobecne riesenie je potom hnusne, ale kedze α je skoro presne 30°, da sa to tam pekne podosadzat. |
|
|
hadanka_na_nedeli.jpg
(Kapitan Bomba) (29.9.2020 20:22)
|
|
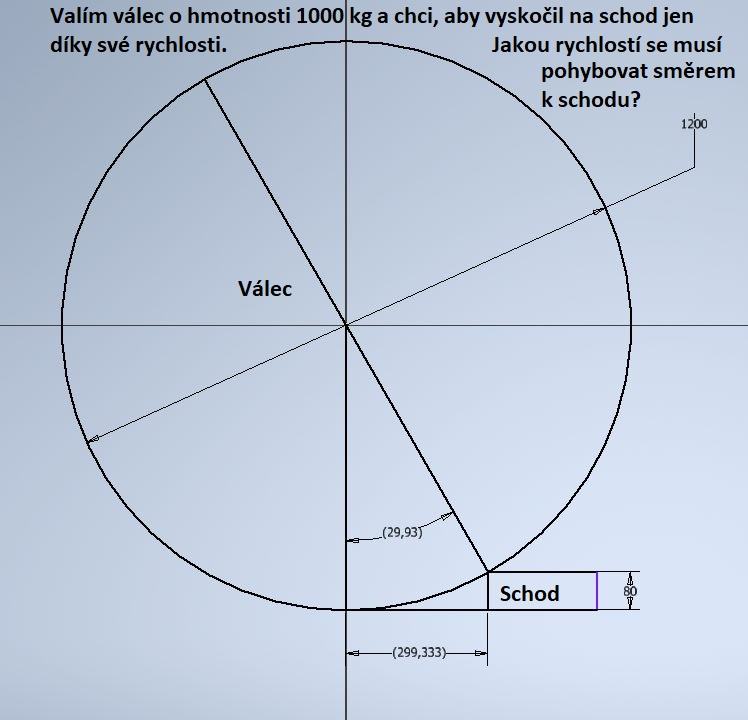
Za predpokladu nuloveho trenia je spravne riesenie priblizne 2,02 m/s bez ohladu na rozlozenie hmoty vo valci. Po naraze sa valec odrazi od rohu pod uhlom 2α (teda asi 60°) a musi dopadnut tak, aby tazisko bolo nad schodom. To vedie na rovnice v_x = v cos 2α a v_y = v sin 2α, odkial x = vt cos 2α a y = vt sin 2α - gt^2/2. Z prvej vyjadrim t a dosadim do druhej, teraz uz iba hladam parabolu, pre ktoru x(0) = 0, x(t) = R cos α, y(0) = 0 a y(t) = 0,08 m a uhol v x(0) = 2α. |
|
|
hadanka_na_nedeli.jpg
(klatom) RP (29.9.2020 12:20)
|
Uloha se mi libi. A mam dalsi reseni, jine nez ty predchozi. Ale nevim, jestli si ty vzorce nepamatuju blbe, je to uz hodne dlouho...  Podle me potrebuju energii ke zdvizeni tunoveho telesa o 8 cm, takze 1000/(10*,0
Podle me potrebuju energii ke zdvizeni tunoveho telesa o 8 cm, takze 1000/(10*,0 , asi 1250 kJ. A pak bych videl rychlost podle E=1/2*m*v^2, takze 1,58 m/s. , asi 1250 kJ. A pak bych videl rychlost podle E=1/2*m*v^2, takze 1,58 m/s. |
|
|
hadanka_na_nedeli.jpg
(Dr.Str.) RP (29.9.2020 0:59)
|
|
Brnonymous má pravdu. Vzhledem k laxnosti zadání se dá počítat s energií nutnou ke zvednutí objektu o osm centimetrů nahoru. Ono se to nebude moc lišit ani v realitě. |
|
|
hadanka_na_nedeli.jpg
(uvazuju) (28.9.2020 23:18)
|
|
je ta kocka ziva nebo mrtva? |
|
|
hadanka_na_nedeli.jpg
(MrdalKrysu) (28.9.2020 19:04)
|
|
Kapitan Bomba: mas pravdu. Respektive jeste by se superpevny schod mohl oprit od deformaci v mene pevne trubce vzniklou po narazu, ale to taky spocitat bez zadanych udaju nejde. 456: Nebo se ujebe konec schodu, ale nerozjebe se cely (nevime, jak je dlouhy) a ta porad nemeni nic na tom, ze se muze a nemusi rozjebat ta skruz. |
|
|
hadanka_na_nedeli.jpg
(456) (28.9.2020 17:44)
|
|
Tak moment. Vzhledem k rozměrům a hmotnosti se jedná o betonovu skruž DN1000. Jsou dvě možnosti: Buď se rozjebe schod, nebo se rozjebe ta skruž. Případně se rozjebe obojí. |
|
|
hadanka_na_nedeli.jpg
(Kapitan Bomba) (28.9.2020 16:41)
|
|
MrdalKrysu: to je uplne jedno, ak nemas trenie, rotacna energia tam nakoniec nemoze mat ziadny vplyv. |
|
|
hadanka_na_nedeli.jpg
(MrdalKrysu) (28.9.2020 15:08)
|
|
Naprosto netusime, jak je ve valci rozlozena hmotnost - je to tenkostenna trubka? Tlustostenna trubka? Plna kulatina? Timpadem nemame zadnou sanci ani odhadnout rotacni energii (pouze strop pro nekonecne hustou a nekonecne tenkostennou trubku). Timpadem muzeme spocitat leda hovne jeste predtim, nez se dostaneme k tomu, kolik energie se disipuje pri srazce. Curacky priklad. |
|
|
hadanka_na_nedeli.jpg
(44tops) RP (28.9.2020 13:01)
|
|
Ach jo.. Tak dlouhá diskuse, a přitom správná odpověď byla hned v prvním komentáři. Chjo. |
|
|
hadanka_na_nedeli.jpg
(Dan Konečný) (28.9.2020 12:41)
|
|
Jste kreténi |
|
|
hadanka_na_nedeli.jpg
(s-hole) (28.9.2020 12:10)
|
|
minimalne Ep=Ek => mgh=(mv^2)/2 => v=(2gh)^0.5 = 1.2528 ms-1 |
|
|
hadanka_na_nedeli.jpg
(,,) (28.9.2020 11:39)
|
|
tdkb: To je ta energie otáčení. |
|
|
hadanka_na_nedeli.jpg
(Kapitan Bomba) (28.9.2020 10:39)
|
|
Ani jeden z vas nema pravdu. Cisto energeticky musi platit mgh = mv^2 / 2 + Iω^2 / 2 = mv^2 / 2 + mv^2/4 = 3/4 mv^2, odtial v = sqrt(4gh/3) = 1.03. Ale take jednoduche to nie je, lebo pri naraze o roh posobi impulz v smere od bodu kontaktu do stredu valca (ak zanedbame trenie, s trenim to je este horsie). |
|
 Komentáře (45)
Komentovat
Nezobrazovat
Komentáře (45)
Komentovat
Nezobrazovat
 Podle me potrebuju energii ke zdvizeni tunoveho telesa o 8 cm, takze 1000/(10*,0
Podle me potrebuju energii ke zdvizeni tunoveho telesa o 8 cm, takze 1000/(10*,0 , asi 1250 kJ. A pak bych videl rychlost podle E=1/2*m*v^2, takze 1,58 m/s.
, asi 1250 kJ. A pak bych videl rychlost podle E=1/2*m*v^2, takze 1,58 m/s.