|
troll_pi.jpg
(Fin-troll) (30.1.2011 11:12)
|
|
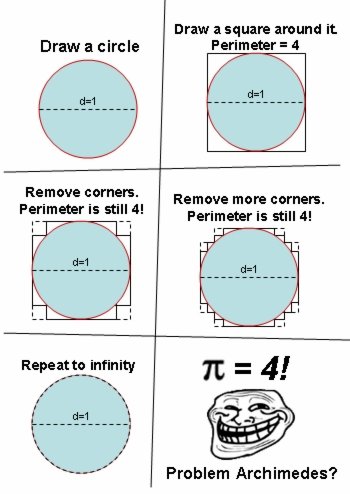
Chyba je v skoku z 4. obr. na 5. obr. Limitou tohto postupu nedostavame kruznicu. Dostavame krivku s "obvodom" 4, ale nepasuje na kruznicu v zmysle limity. Existuju podobne postupy ako spocitat pi, ale je nutne volit spravne postupnosti utvarov. Napriklad limita obvodu pravidelneho n-uholnika pre n iduce do nekonecna. |
|
|
troll_pi.jpg
(.) (17.11.2010 12:52)
|
|
na zacatku me nenapadlo, co tu bude za diskusi. obzvlaste s cim vsim to tu lidi budou zkouset davat do souvislosti...
-pi vychazi z jednotkovyho geometrickyho primitiva
-tohle je jakasi aproximace kruznice v rastru (at bude rastr sebejemnejsi, nikdy to nebude kruznice - za predpokladu, ze zanedbame algoritmy na interpolaci barev za ucelem zjemnovani barevnych prechodu) |
|
|
troll_pi.jpg
(dsf) (16.11.2010 23:17)
|
Aha nedošlo mi, že to nebude zformátované  . Pořadová čísla 1., 2., 3. jsou číslované body mé úvahy |
|
|
troll_pi.jpg
(dsf) (16.11.2010 23:10)
|
|
Pánové, pokud mám někde v úvaze chybu, tak mě opravte.
1. obvod čtverce (a) > délka jemu vepsané kružnice (b). Tj. 4 > pi
2. provádíme úpravy při nichž se obvod opsaného útvaru (a) nemění ani se nemění délka kružnice (b).
3. provedeme nekonečno takových úprav při nichž se délky nemění, takže pro n=nekonečno logicky platí, a=4, b=pi, a > b, tj. 4 > pi. |
|
|
troll_pi.jpg
(kolol) RP (16.11.2010 20:37)
|
Hlavne je zabavne, jak to nekteri zacinaji resit zase uplne od zacatku  Klidne pridejte dalsi dve stovky komentaru, treba padne rekord |
|
|
troll_pi.jpg
(JirkaCV) (16.11.2010 19:37)
|
|
Tak to je typická práce trolla. Přijde, nadhodí nějakou ptákovinu a pak z povzdálí sleduje, jak se rozhořívá flame. Někdy si říkám, jestli on nebude placenej jednou nejmenou společností. |
|
|
troll_pi.jpg
(klokan) (16.11.2010 19:22)
|
ultrasfan: no a prave v tom, ze nedostanes tecny (nepujdes jinak nez vodorovne nebo zvisle) je to troleni 
To mas to same jako by si chtel prejit z jednoho rohu ctverce do druheho... Kdyz pojedes po uhlopricce tak prejdes vzdalenost sqrt(2) = 1.41421. Kdyz pojedes po libovolnem pocte malych vodorovnych a svislych useku, tak ve vodorovnem i svislem smeru prejdes vzdalenost 1, takze dohromady 2. To mas to same jako by si sel po obvodu ctverce. |
|
|
troll_pi.jpg
(ultrasfan) RP (16.11.2010 19:11)
|
|
to mas pravdu, ale trollim postupom dotycnice nedostanes |
|
|
troll_pi.jpg
(klokan) (16.11.2010 19:04)
|
|
Trol tim ctvercem aproximuje obsah kruhu a ne jeho obvod.
Vsimnete si ale, ze ty ctvercove strany jsou jenom vodorovne, nebo zvisle. Obvod se neda aproximovat pouze takovymi useky, ale je potreba pouzit tecny ke kruznici. Kdyz kruznici zabalime do pravidelneho 3uhelniku, mame obvod trojuhelniku 5,19615 pro ctverec je to jako na druhem obrazku 4, ale pak treba pro sestiuhelnik je to uz jenom 3,4641... Pro obecny n-uhelnik je to n*tangens(pi/n) napr. n=100 je to 3.14263 a toto cislo uz se hodne blizi pi |
|
|
troll_pi.jpg
(Umpire) RP (16.11.2010 18:10)
|
|
hle, prestal sem cist komentare na 5. strane, ale do ty doby vsem unikla skutecnost, ze v nekonecnu to tak je se vsim, jako rovnobezky kdyz se sejdou v nekonecnu atd. takze misto kruznice by tam moh bejt trojuhelnik a dalo by se tvrdit ze v nekonecnu maj stejnej obsah i obvod... |
|
|
troll_pi.jpg
(ultrasfan) RP (16.11.2010 17:56)
|
|
myslim, ze tu je zakladny problem, a to, ze aj keby to zmensoval "do nekonecna" nikdy to nebude kruh, ale "hranaty kruh"... to neustale zmensovanie sa nazyva Fraktaly, resp mi ich to dost v principe pripomina... teda podla mna, aj keby sa veeeeelmi priblizil k tomu tvaru kruhu tak ten obvod bude 4 oproti "klasickych" PI (3,14), pretoze nech tie hrany akokolvek zmensuje, vzdy su ich strany dokopy dlhsie ako ich uhlopriecka (pre zjednodusenie, neviem ako nazvat kruh prechadzajuci tymi vrcholmi.....) |
|
|
troll_pi.jpg
(Ebo) RP (16.11.2010 17:53)
|
|
kurňa .. 154 komentářů.. tohle vědět, tak jsem to tam na serveru nechal ležet |
|
|
troll_pi.jpg
(Loki) RP (16.11.2010 17:45)
|
|
trol tvar (uvodny stvorec) nie je kruznica. ak odrezeme rohy, tak stale nemame kruznicu. ak dalsie, tak tiez nemame kruznicu, atd.... odrezali sme nekonecno rohov a stale nedostaneme kruznicu. pretoze troll ukazuje ze rezanim jedneho rohu kruznicu nedostaneme... ci? |
|
|
troll_pi.jpg
(moo) RP (16.11.2010 17:30)
|
|
dufam, ze presne toto autor chcel vyvolat |
|
|
troll_pi.jpg
(Tomsus) RP (16.11.2010 16:54)
|
|
Ttxman: jenomze tohle v korektni matematice nefunguje, protoze neni nejmensi realne cislo x>0, protoze realna cisla nejsou dobre usporadana mnozina, tj. nelze pro kazde cislo najit jejiho nasledovnika (dokonce v R pro kazde cislo). To co k tomu pisou na ceske wiki je (predpokladam) matematika pocatku 18. stoleti. Ne, ze by uz tam neznali uzasne veci, ale spoustu veci zase delali velmi naivne. |
|
