|
kolejnice.png
(Ellrohir) RP (4.3.2011 20:32)
|
koukám, že je tady spousta lidí svázanejch Euklidovskou geometrií  |
|
|
kolejnice.png
(Tom) (4.3.2011 18:34)
|
|
Dr.Str.: tezko mohou podlehat deformaci prostoru, kdyz jsou nehmotne ... gravitace pusobi na hmotne veci(atomy, fotony etc.) ...
A proc zrovna cerna dira? Jejich hustota v prostoru je mala, kvuli jejich hmotnosti ... pravdepodobnost je mala, ze se zrovna trefis do rozmerove relativne male cerne diry ... |
|
|
kolejnice.png
(eratni) RP (4.3.2011 16:25)
|
zasmál jsem se, takže líbí, i když je to píčovina  |
|
|
kolejnice.png
(Stín) RP (4.3.2011 16:08)
|
|
Tomsus: +100 internetz. Něco takového jsem chtěl slyšet. Lobačevského geometrie je mi zatím nenámá, zkusím to změnit |
|
|
kolejnice.png
(Peter) (4.3.2011 15:54)
|
|
@nx2k no, keby bola, tak podľa obrázku by v škole hovorili pravdu.
a btw, v perspektívnom zobrazení sa rovnobežky zbiehajú, a stretávajú sa v nejakom bode, ktorý nie je nekonečno |
|
|
kolejnice.png
(Mipi) RP (4.3.2011 15:52)
|
|
Dle hustopokončevskeho zákona jsou dvě rovnoběžky trojúhelníky a jejich vnitřní součet úhlů se blíží nekonečnu. |
|
|
kolejnice.png
(Tomsus) RP (4.3.2011 15:48)
|
Tak jsem kvuvli vam otevrel skripta na teoretickou fyziku a podival se na ulohu s nadpisem "Poincareuv model Lobacevskeho geometrie". Jde o to, ze mate osy x a 1/y. Potom jakoby na ose x (tj y=0) jakoby lezi nekonecno. Primky jsou pulkruznice se stredem na ose x a to nejlepsi -- rovnobezky jsou dve polokruznice, ktere maji spolecny bod na ose x  (Zajimave je, ze pak si muzete zvolit primku p, bod P, ktery nelezi na primce p a timto bodem P pak muzete vest dve ruzne rovnobezky s primkou p (Zajimave je, ze pak si muzete zvolit primku p, bod P, ktery nelezi na primce p a timto bodem P pak muzete vest dve ruzne rovnobezky s primkou p  |
|
|
kolejnice.png
(nx2k) RP (4.3.2011 15:02)
|
|
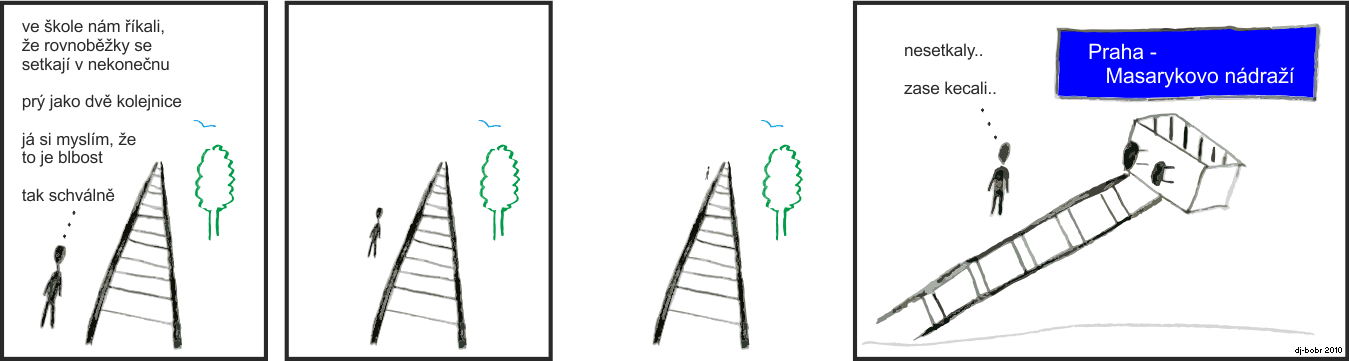
Má tam chybu, Masaryčka není nekonečno. |
|
|
kolejnice.png
(xmefik) RP (4.3.2011 14:39)
|
|
Rovnoběžky se v nekonečnu nesetkají, to tvrzení IMHO nemá matematicky vůbec smysl. Vzdálenost mezi rovnoběžkami je v libovolné reálné vzdálenosti od předem definovaného počátku konstantní. |
|
|
kolejnice.png
(Dr.Str.) RP (4.3.2011 14:39)
|
No, fyzik by asi řekl, že dvě rovnoběžky mířící jedním směrem pravděpodobně po dost velké, ale přesto měřitelné vzdálenosti skončí obě v černé díře a pomocí ohnutého prostoru zkolabují do jednoho bodu  |
|
|
kolejnice.png
(JLo) (4.3.2011 14:31)
|
|
To není geometrie ale výtvarka - v perspektivní projekci se rovnoběžky jiné než na ploše papíru střetávají. |
|
|
kolejnice.png
(stráťa) (4.3.2011 14:26)
|
Stín: Taky to nechápu, pokud se někde setkaj tak nemůžou být rovnoběžný.  |
|
|
kolejnice.png
(Stín) RP (4.3.2011 14:04)
|
|
Já bych matfyzáky spíš poprosil, aby vysvětlili proč by se měly kdy setkat... (v Eukleidovské geometrii samozřemě, jestli to platí v jiné nechám se poučit) |
|
|
kolejnice.png
(SUK) RP (4.3.2011 14:04)
|
Organic: v tomhle asi slo o to, ze kolejnice nejsou primky (tzn od nekonecna do nekonecna). A s homogennima souradnicema maj i rovnobezky prusecik  |
|
|
kolejnice.png
(ou) (4.3.2011 13:46)
|
|
42 |
|
 Komentáře (17)
Komentovat
Nezobrazovat
Komentáře (17)
Komentovat
Nezobrazovat


 (Zajimave je, ze pak si muzete zvolit primku p, bod P, ktery nelezi na primce p a timto bodem P pak muzete vest dve ruzne rovnobezky s primkou p
(Zajimave je, ze pak si muzete zvolit primku p, bod P, ktery nelezi na primce p a timto bodem P pak muzete vest dve ruzne rovnobezky s primkou p 








