|
programmers_vs_mathematitians.jpg
(hynek) (16.1.2021 17:35)
|
|
Když se matematikům nelíbí X= ∞ nebo X= -∞ , tak programátorům by stačilo ke spokojenosti x = 2.0 ** 53 nebo x = - 2.0 ** 53 - 4.0 |
|
|
programmers_vs_mathematitians.jpg
(KarlosPepinator) RP (16.1.2021 14:05)
|
|
A to jako odkdy? |
|
|
programmers_vs_mathematitians.jpg
(Mem) RP (16.1.2021 13:31)
|
Proč by VBA mělo umět ++, když má Inc. To zase přišel odborník  |
|
|
programmers_vs_mathematitians.jpg
(KarlosPepinator) RP (16.1.2021 13:06)
|
|
Boha jeho to je banda kokotů... OP chtěl jen poukázat na to, že ve zdrojáku je x=x+1 naprosto běžná inkrementace (např VBA neumí x++), zatímco matematik je z toho vprdeli asi jako vy všichni tady. |
|
|
programmers_vs_mathematitians.jpg
(Pepin22) (13.1.2021 22:26)
|
///: já se rozhodně nikomu nevysmívám, a jestli jo, tak se omlouvám. Ale jen jsem hájil svou teorii, že nekonečno by té rovnice pasovalo, až to dospělo do úplného absurdna |
|
|
programmers_vs_mathematitians.jpg
(///) (13.1.2021 22:03)
|
Pepin22: Machrovat? Eh? Ty se tu ostatním vysmíváš za „matematiku základní školy“ a plácáš blbosti k tomu. Já jen chtěl dát real life příklad, kdy na tom extrémně záleží. Pokud chceš rozumnější (stejný) příklad, tak si vem třeba Lebesgueovu míru na intervalu [0,1] – rovnoměrné rozdělení a základ absolutně spojitých rozdělení. Všechna čísla mají stejnou pravděpodobnost, přesto pravděpodobnost racionálního čísla je 0, iracionálního 1. Racionální i iracionální číslo je jev možný (v sigma algebře).  |
|
|
programmers_vs_mathematitians.jpg
(Pepin22) (13.1.2021 17:26)
|
|
///: pokud budeš plavat v nekonečném moři plném hoven, kde na hovno narazíš každý metr, tak tam těch hoven bude stejně nekonečné množství jako když na to hovno narazíš každé 2 metry. To je mohutnost ve vztahu k nekonečnosti. |
|
|
programmers_vs_mathematitians.jpg
(Pepin22) (13.1.2021 17:19)
|
|
///: A nějaký zajímavější příspěvek do diskuze, než že machruješ s tím, že opakuješ co jsi si tu přečetl nemáš? |
|
|
programmers_vs_mathematitians.jpg
(///) (13.1.2021 14:31)
|
Pepin22: Nekonečno je jen jedno? He? Tvářit se, že množina reálných čísel je stejně mohutná jako množina racionálních čísel, je stejné jako říkat totálně vyžraným holkám, že jsou curvy.  |
|
|
programmers_vs_mathematitians.jpg
(X!) (13.1.2021 12:11)
|
|
@456:
A co teprve x = x^2 +1
x = (-1)^(1/3) |
|
|
programmers_vs_mathematitians.jpg
(Pepin22) (13.1.2021 12:05)
|
Je pravda, že už jsme se dostali do hodně abstraktních pojmů (a asi bych se hádal i s autorem tohodle článku  ) Každopádně díky za plodnou debatu, ale asi si furt budu trvat na tom, že nekonečno +/- cokoliv je furt nekonečno. Dle mého soudu je tohle totiž podstata nekonečna. ) Každopádně díky za plodnou debatu, ale asi si furt budu trvat na tom, že nekonečno +/- cokoliv je furt nekonečno. Dle mého soudu je tohle totiž podstata nekonečna. |
|
|
programmers_vs_mathematitians.jpg
(f35) (13.1.2021 11:51)
|
|
https://www.matfyz.cz/clanky/matykani-vii-moje-nekonecno-je-vetsi-nez-to-tvoje eeeh |
|
|
programmers_vs_mathematitians.jpg
(Pry_) (13.1.2021 11:50)
|
|
Pepin22: Je mi to líto, ale mýlíš se. Stručně .. nekonečen je nekonečně mnoho a mohou mít různé velikosti. Např. celých čísel u určitě méně než reálných, když se nad tím zamyslíš. Viz "mohutnost množiny" na wikipedii |
|
|
programmers_vs_mathematitians.jpg
(Pepin22) (13.1.2021 11:30)
|
|
Filipes: pokud z množiny sudých čísel odebereš jedno číslo, stále bude obsahovat nekonečné množství čísel a úplně stejně to dopadne pokud to uděláš s množinou reálných čísel. Nekonečno je jen jedno a není žádné poloviční nebo dvojnásobné nekonečno. |
|
|
programmers_vs_mathematitians.jpg
(Filipes) RP (13.1.2021 11:08)
|
(GarryR):  (Pepin22): No ono záleží na definici toho nekonečna - například množina reálných čísel je 2x větší, než množina sudých čísel (i když jsou obě nekonečné)
(Pepin22): No ono záleží na definici toho nekonečna - například množina reálných čísel je 2x větší, než množina sudých čísel (i když jsou obě nekonečné)  Takže jen tak od boku střelit, že ta jednička nic nezmění je dle mého hloupost) Takže jen tak od boku střelit, že ta jednička nic nezmění je dle mého hloupost) |
|
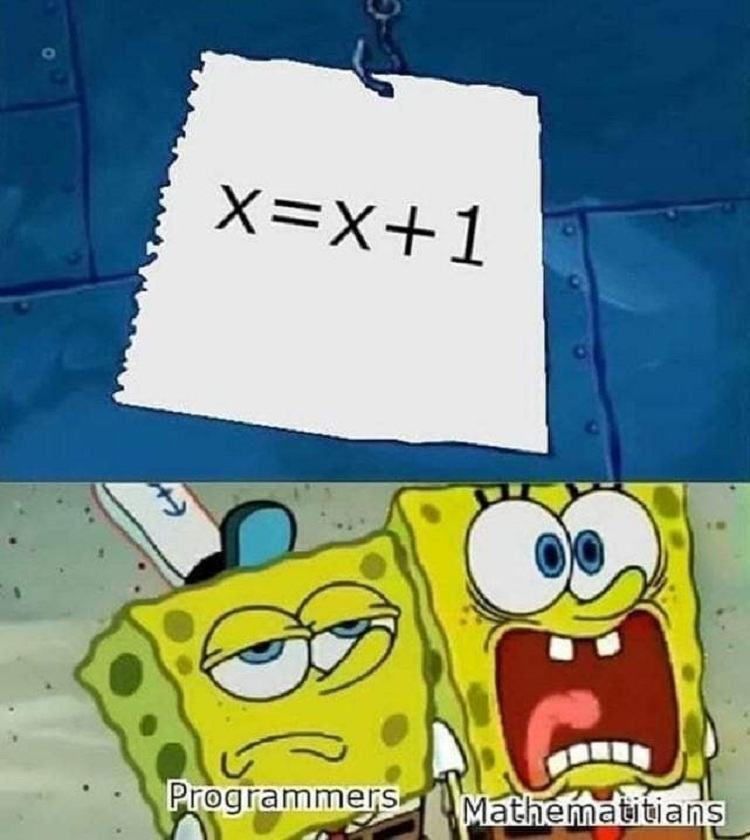 Komentáře (34)
Komentovat
Nezobrazovat
Komentáře (34)
Komentovat
Nezobrazovat




 ) Každopádně díky za plodnou debatu, ale asi si furt budu trvat na tom, že nekonečno +/- cokoliv je furt nekonečno. Dle mého soudu je tohle totiž podstata nekonečna.
) Každopádně díky za plodnou debatu, ale asi si furt budu trvat na tom, že nekonečno +/- cokoliv je furt nekonečno. Dle mého soudu je tohle totiž podstata nekonečna.  (Pepin22): No ono záleží na definici toho nekonečna - například množina reálných čísel je 2x větší, než množina sudých čísel (i když jsou obě nekonečné)
(Pepin22): No ono záleží na definici toho nekonečna - například množina reálných čísel je 2x větší, než množina sudých čísel (i když jsou obě nekonečné)  Takže jen tak od boku střelit, že ta jednička nic nezmění je dle mého hloupost)
Takže jen tak od boku střelit, že ta jednička nic nezmění je dle mého hloupost) 




