Odebírat | ||
|
Obrázek 'asymptotic portals' (skylajner_nepr) (4.3.2014 22:13) | reagovat |
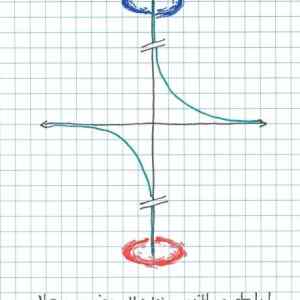
| Tak tohle sem prošel ještě než tu byl flame... tak moje reakce na flame: deskriptivně vzato, Hyperbola je kružnice, která prochází osou nekonečna (Parabola se nekonečna dotýká) ...a ony dvě části, jež sečna(nekonečno) tvoří jsou ony dvě "půlky" hyperboly. To znamená, že by to mělo fungovat, nicméně nemůžu říct jestli takhle nebo přes další dva portály na ose x | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (Abdul_Hasan) RP (3.10.2011 10:54) | reagovat |
Každý kdo hrál portal ví, žew stačí, aby ty portaly nebyly přesně nad sebou, ale lehce vychýlené, pak bude graf pokračovat v jedné lajně  |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (slaverr) (2.10.2011 23:50) | reagovat |
| fail, protože portál by musel být na místě kde graf protíná osu, nebo kde se aspoň dotýká. funkce se přibližuje ale nikdy se nedostane bliž než na minimální vzdálenost | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (Jur) RP (1.10.2011 14:06) | reagovat |
| aha s tym Df by som aj tak tvrdil ze to bude stale bezny definicny obor R/{0} lebo y=1/x nieje definovane iba v 0. a vypocitat y v ktoromkolvek bode by nema byt problem za predpokladu ze vies suradnice portalu a su dobre definovane(napr su rovnobezne s osou x a pociatocne a koncove x-ove suradnice su totozne) potom to nieje ani velmi zlozita transformacia a to sa uci uz v zakladoch algebry ale ak by to bolo zlozitejsie tak to by som si netrufol riesit bez nejakeho lepsieho studia a vlastnej teorie portalov | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (Gotcher) (1.10.2011 13:49) | reagovat |
| Tím pádem by ale bylo nutné omezit Df. Df = R/{0+-d} (d je nějaké to odsazení delta). | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (Gotcher) (1.10.2011 13:47) | reagovat |
|
Jur: Obor hodnot? Inu, bude nejspíš dán omezen těmi portály ne? Čili Hf = (portal1.y,portal2.y) otevřený interval proto, že na pozici portálu už těžko určíš, kde vlastně jsi. |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (Jur) RP (1.10.2011 13:39) | reagovat |
ak sa mylim budem vdacny za kazdu pripomeinku
dakujem
ale je to zaujimave to by mohla byt dobra diplomova praca  |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (Jur) RP (1.10.2011 13:38) | reagovat |
| trochu studujem matematiku tu je niekolko moznosti ktore by platili a zopar poznamok: pre jednoduchost predpokladajme ze to je graf funkcie y=1/x 1. asyptota tejto funkcie by sa zobrazovala stale blizsie a blizsie k osy y a znova a znova by isla do portalu 2. neviem ako funguje portal tak neviem ci naozaj pohlti os a cast polroviny za nim toto by bolo zaujimave skumat 3. ak by bol ten druhy portal s vymenenymi stranami nebola by to uz funkcia ale pripominalo by to parabolu ktorej osou je os x 4. Df=R Hf=? | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (Noamuth) RP (1.10.2011 11:44) | reagovat |
| a potom ako sa uhne tá čiara od zvislej ? | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (misof) RP (1.10.2011 9:35) | reagovat |
Celé to môže fungovať priamo tak ako je to nakreslené, treba len červený portál vyrobiť otočený o 180 stupňov oproti modrému a tým vymeniť vľavo a vpravo  |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (Blah_kdo_si_sakra_registroval_muj_blah?) (1.10.2011 9:26) | reagovat |
|
Tady je to samy "matematyk", vidim. / A pak ze ma 1/x neodstanitelnou nespojitost. Deleni nulou je vyreseno! |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (testa) (1.10.2011 9:13) | reagovat |
| ale ho*no, obrazok ma pravdu, ked si vezmeme zakryvenie priestoru tak cela os y je vlastne kruznica (podobne os x a priestor ktory tvoria je vlastne gula) | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (Hm) (1.10.2011 8:27) | reagovat |
|
Zmysel tento obrazok dava vtedy pokial uvazime, ze niekde vyssie po osi y existuje dalsi cerveny portal, ktory je spojeny s modrym portalom na obrazku a niekde nizsie po osi y zase existuje dalsi modry portal, ktory je spojeny s cervenym portalom na obrazku. Ale v ziadnom pripade neexistuje spojenie medzi portalmi, ktore su nakreslene. |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (SUK) RP (1.10.2011 7:54) | reagovat |
|
ty portaly jsou jakoze v nekonecnu. A nebo jsou posunuty |
||
|
|
||
|
|
Obrázek 'asymptotic portals' (Momo) RP (1.10.2011 7:42) | reagovat |
| musis naklonit hlavu dolava | ||
|
|
||
|
|
Obrázek 'asymptotic portals' (BG) RP (1.10.2011 2:49) | reagovat |
| kazdy matematyk hned vidi ze je to pycovina.... ta krivka ktora zobrazuje funkciu nalavo od osy y nema nic spolocne s tou krivkou napravo.... takze aby to malo byt spravne, tak medzi portalmi bude nejkonecne vela zvislych kriviek zhora nadol, stale blizsie k ose y... a kedze to nema matematicky joke, ani matematicky vyznam, tak to nema vyznam ziadny... | ||
|
|
||